This topic summarizes how spatial predicates are defined:
- Background
- Boundary, Interior, and Exterior
- String Representations of Intersection Matrices
- Definitions of Predicate Attributes
For definitive documentation on spatial relations, please consult the OGC documentation on spatial relations.
Click here to see an example that illustrates different spatial relationships.
Spatial Predicates
Background
The definitions of each Predicate attribute are given in the tables included under this heading. This section also gives specific definitions of boundaries, exteriors, and interiors as they apply to specific feature types and explains the concept of an intersection matrix.
Each feature – whether it's a point, line, or polygon – has a definition of an INTERIOR, BOUNDARY, and EXTERIOR. The EXTERIOR is everything that is not on the BOUNDARY or the INTERIOR.
Spatial relations are undefined for geometries that are not OGC valid or aggregate geometries.
Boundary, Interior, and Exterior
| BOUNDARY | Points | Empty set. |
| Lines |
CURVE_BOUNDARY_RULE ENDPOINTS_MOD2 The boundary is the set of all endpoints that occur an odd number of times. For a simple linear feature (that is, not a multicurve), this means the boundary is comprised of the start and end points, unless the line is closed (the start and end are the same point), in which case the boundary is the empty set. (This is the default if CURVE_BOUNDARY_RULE is unspecified.) CURVE_BOUNDARY_RULE ENDPOINTS_ALL The boundary is the set of all endpoints, regardless of the number of times they occur in the geometry. |
|
| Polygons | The border of a polygon, including the border of the holes. | |
| INTERIOR | Points | The point location. |
| Lines | The entire line except its boundary as determined above. | |
| Polygons | The inner surface of the polygon. |
Dimensionally Extended 9 Intersection Matrix
The comparison of two features produces a 3 x 3 matrix known as the Dimensionally Extended 9 Intersection Matrix (DE-9IM), shown below:
| candidate | ||||
| interior | boundary | exterior | ||
| base | interior | c0 | c1 | c2 |
| boundary | c3 | c4 | c5 | |
| exterior | c6 | c7 | c8 | |
The value of each element of the matrix indicates the dimension of the geometry produced by intersecting the given parts of the two features. The dimension is one of the following:
-1 there is no interaction
0 the intersection produces a point
1 the intersection produces a line
2 the intersection produces a surface
So for instance, if c1 is 1, then the intersection of the base's interior with the candidate's boundary produces a line. This could occur when both features are polygons and they overlap.
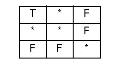
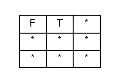
Each of the predicates can be defined in terms of what the intersection matrix of the two features must look like. For this, use a pattern matrix. Each element of the pattern matrix can be one of the following:
* the value of this element may be anything (-1, 0, 1, or 2)
T the value of this element must be 0, 1, or 2
F the value of this element must be -1
0 the value of this element must be 0
1 the value of this element must be 1
2 the value of this element must be 2
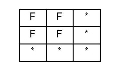
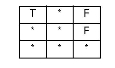
The pattern matrix for the disjoint predicate is:
| F | F | * |
| F | F | * |
| * | * | * |
This means that neither feature's interior or boundary may interact with the other's interior or boundary.
String Representations of Intersection Matrices
Any intersection matrix can be represented as a 9-character string. To generate the string representation of a particular intersection matrix, take each element starting from the top-left, going right-to-left for each row.
For example, the string representation of the intersection matrix for the disjoint predicate (as seen above) is “FF*FF****”.
Definitions of Predicate Attributes
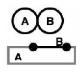
Each of the supported predicates is described below, along with some associated examples and pattern matrices. Note that the examples are not exhaustive: there may be entirely different situations where a given predicate is true. In the examples, the base is labeled "A" and the candidate is labeled "B".
| Predicate | Example | Description | Pattern Matrix |
|---|---|---|---|
| INTERSECTS | The two features are not disjoint, as defined below. | ||
| DISJOINT |
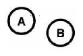
|
The boundaries and interiors do not intersect. |
|
| EQUALS |

|
The features have the same boundary and the same interior. |
|
| TOUCHES |
|
The boundaries may intersect or one boundary may intersect the other interior. The interiors do not touch. Undefined for point/point. |
|
|
or 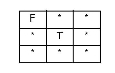
|
|||
|
or 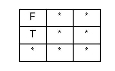
|
|||
| CROSSES |
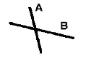
|
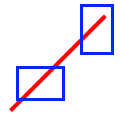
The interiors intersect and the base’s interior intersects the candidate’s exterior. Or in the case of line/line, the intersection of the interiors forms a point. Undefined for point/point or area/area. Undefined for aggregate/multi geometries. |
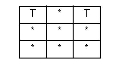
|
|
or, for two lines: 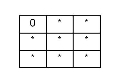
|
|||
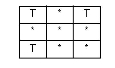
| OVERLAPS |
|
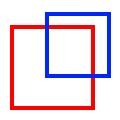
The interiors intersect, but neither feature is contained by the other, nor are the features equal. Undefined for point/line, point/area, or line/area. Undefined for aggregate/multi geometries. |
|
|
or, for two lines: 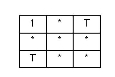
|
|||
| CONTAINS |
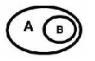
|
The interiors intersect and no part of the candidate's interior or boundary intersects the base's exterior. It is possible for the boundaries to intersect. (inverse of WITHIN) |
|
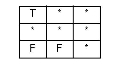
| WITHIN |
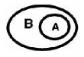
|
The interiors intersect and no part of the base's interior or boundary intersects the candidate's exterior. It is possible for the boundaries to intersect. (inverse of CONTAINS) |
|
| <DE-9IM string> |
In addition to the predicates listed above, spatial relations can also be specified using a string representation of an intersection matrix. Undefined for aggregate/multi geometries. |
||
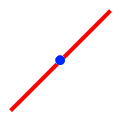
Spatial Relationship Examples
| Spatial Relations | Base | Candidates | |||

|

|

|
|||
| Intersects | Contains |

|

|

|

|

|
|

|

|
||

|

|

|

|
||
| Crosses |

|

|

|

|
|

|

|

|
|
||

|

|

|

|
||
| Equals |

|

|

|

|
|

|

|

|

|
||

|

|

|

|
||
| Overlaps |

|

|

|

|
|

|

|

|

|
||

|

|

|
|
||
| Touches |

|

|
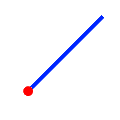
|
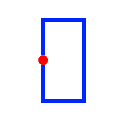
|
|

|

|

|
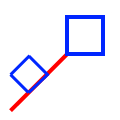
|
||

|
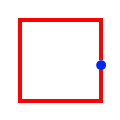
|
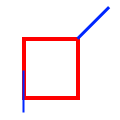
|
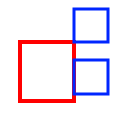
|
||
| Within |

|

|
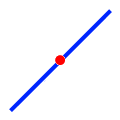
|

|
|

|

|

|

|
||

|

|

|

|
||
| Disjoint |

|

|
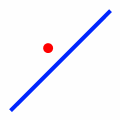
|
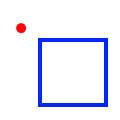
|
|

|
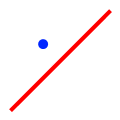
|

|

|
||

|

|

|

|
||
Search FME Knowledge Center
Search for samples and information about this transformer on the FME Knowledge Center.