RubberSheeter

Performs warping operations on the spatial coordinates of features. Using inverse distance weighting, RubberSheeter adjusts a set of observed features so they more closely match some set of reference features. This transformer applies a different transformation to each Observed vertex, depending on its distance to nearby Control vectors. It produces good corrections when the distortions in the Observed data are not constant.

Input Features

Two sets of features must be routed into this transformer:

• Features that enter through the Control port represent the control features used to compute the corrections.
• Features that enter through the Observed port are the features that will be corrected.

Each Control feature represents a control vector whose start point is at some location in the original Observed data space, and whose end point is at the corresponding location in the desired output data space. The control vector represents the correction required to go from the observed vertex to the desired vertex. (Control vectors with only one point are interpreted as a requirement that this location not change from the observed dataset to the reference dataset. This is often referred to as a tie point.)

Optionally, lines may be input as Constraint features to this transformer. These lines will be treated as boundaries, across which control vectors will have no influence on points of observed features. If the "line of sight" from a point on an Observed feature to the starting point of a Control vector crosses a Constraint line, that control vector will not affect the resulting warped position of the point in question. If the line of sight touches the end of a Constraint line, or either the Control vector or Observed point is actually located on the Constraint line, then the Control vector will still influence the observed point.

Note: This transformer does not currently support raster geometry.

Output Ports

The modified Observed features are output via the Corrected port.

Parameters

Comparison to the AffineWarper

The AffineWarper transformer provides similar functionality but computes an affine (scale, rotation, and offset) transformation based on Control vector features and applies this transformation to the Observed features to generate output. This makes the AffineWarper more appropriate for cases when the entire set of Observed data requires a single transformation.

Case Study

Click here to read how FME’s RubberSheeter was used to combine Manukau City Council’s existing parcel-dependent cadastral data with a newer “survey accurate” national digital cadastre.

Common Questions

I have a line feature only some of whose points fall inside the Max Distance. How will it be warped? Only vertex points that lie inside the Max Distance will get warped. Therefore, part of your line will be warped, part of it will not.

Why doesn't FME warp the entire feature when one of its points falls inside the Max Distance? Because this could causes topological networks to become broken. Working on a point-by-point basis, connections will never be broken because the common point on the connecting feature will also get warped (even if the rest of that feature doesn't).

Example

                

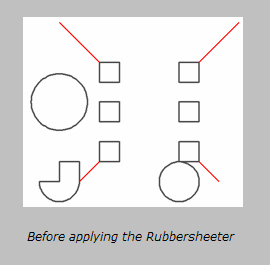
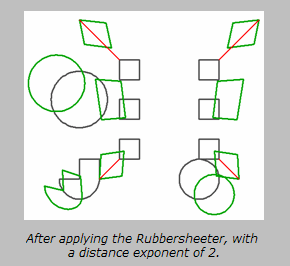
Editing Transformer Parameters

Using a set of menu options, transformer parameters can be assigned by referencing other elements in the workspace. More advanced functions, such as an advanced editor and an arithmetic editor, are also available in some transformers. To access a menu of these options, click beside the applicable parameter. For more information, see Transformer Parameter Menu Options.

Transformer Categories

Geometric Operators

FME Licensing Level

FME Professional edition and above

Search FME Knowledge Center

Search for samples and information about this transformer on the FME Knowledge Center.