Affiner

Performs an affine transformation (such as offset, rotate, or scale) on the coordinates of the feature.

Typical Uses

Moving, scaling, and rotating 2D geometry.

How does it work?

The Affiner receives features with any geometry type and moves their x and y coordinates according to a specified affine transformation.

An affine transformation is a mathematical method of modifying geometry that:

Preserves lines/collinearity: all points on a straight line are still on a straight line after transformation.
Preserves parallelism: lines that are initially parallel are still parallel after transformation.
May not preserve angles, lengths, or areas, depending on the type of transformation performed.

Scaling, mirroring, rotating, shearing, and translating (relocating or offsetting) are all affine transformations. They can be performed singly or in combination.

The Affiner performs 2D transformations, using this formula:

x' = Ax + By + C

y' = Dx + Ey + F

Where (x,y) are the input coordinates and (x',y') are the transformed output coordinates.

	Description	Formula/Coefficients	Example*
Translate	Move the geometry a fixed distance.	x' = 1x + 0y + C y' = 0x + 1y + F Simplified: x' = x + C y' = y + F C = horizontal (x) offset F = vertical (y) offset	x' = 1x + 0y + 5 y' = 0x + 1y + 5
Scale	Shrink or enlarge the geometry.	x' = Ax + 0y + 0 y' = 0x + Ey + 0 Simplified: x' = Ax y' = Ey A = horizontal (x) scale factor E = vertical (y) scale factor	x' = 1.5x + 0y + 0 y' = 0x + 1.5y + 0
Rotate	Rotate the geometry around the origin.	x' = cos(ϴ)x + −sin(ϴ)y + 0 y' = sin(ϴ)x + cos(ϴ)y + 0 Simplified: x' = cos(ϴ)x − sin(ϴ)y y' = sin(ϴ)x + cos(ϴ)y ϴ = Angle in degrees A = cos(ϴ) B = −sin(ϴ) (Note negative value) D = sin(ϴ) E = cos(ϴ)	Rotate 30 degrees: x' = 0.866025x + -0.5y + 0 y' = 0.5x + 0.866025y + 0
Shear	Offset geometry in proportion to its x and y coordinates.	x' = 1x + By + 0 y' = Dx + 1y + 0 Simplified: x' = x + By y' = y + Dx	x' = 1x + 1.25y + 0 y' = 0x + 1y + 0

* Note these examples use geometry with an origin of 0,0 at the lower left corner of the polygon.

Geographic Features and Affine Transformations

The origin (0,0) of geographic features is generally at a distance from the geometry itself, and so affine transformations can produce large location shifts, in particular when scaling or rotating.

Examples

Example: Affine transformations on geographic features

In this example, we will perform various transformations on a set of neighborhood polygon features, which are in a UTM projection with ground units in meters.

The features are routed into an Affiner.

Translating Features East and North

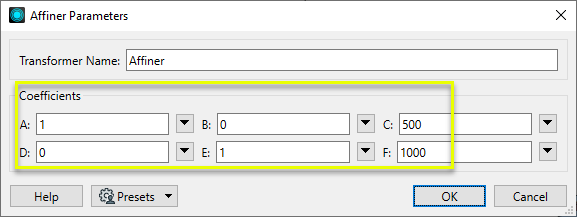
In the parameters dialog, we enter coefficients to move the features 500 meters east and 1000 meters north.

x' = 1x + 0y + 500
y' = 0x + 1y + 1000

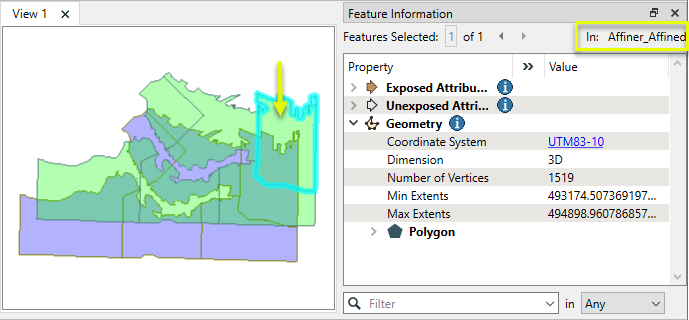
The output features have been translated.

Scaling Features

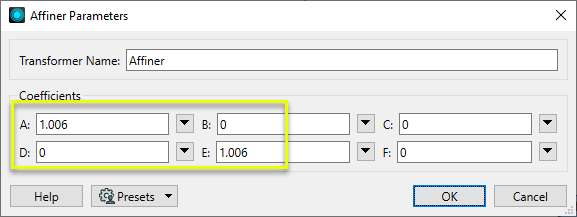
In the parameters dialog, we enter the coefficients to scale the features up by a factor of 1.006.

x' = 1.006x + 0y + 0
y' = 0x + 1.006y + 0

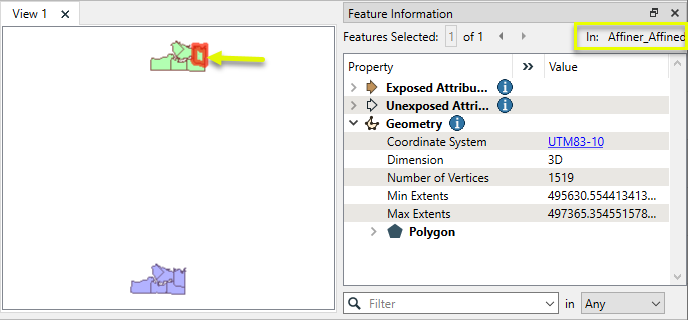
Note that even a small scale factor such as this can produce large shifts in position when the features are georeferenced.

Rotating Features

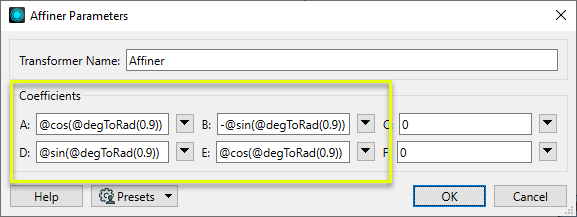
In the parameters dialog, we enter the coefficients to rotate the features by 0.9 degrees.

We could enter explicit parameter values, but will use expressions to calculate the coefficients.

Note that the math functions @cos() and @sin() expect radians (not degrees), and so we add the @degToRad() function to convert our rotation angle to radians.

x' = cos(0.9)x + -sin(0.9)y + 0
y' = sin(0.9)x + cos(0.9)y + 0

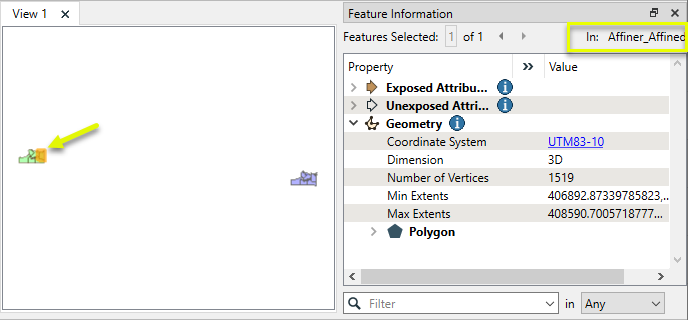
Note that even a small rotation such as this can produce large shifts in position when the features are georeferenced, as they are being rotated about their origin (0,0) which is at a distance.

Usage Notes

To perform affine transformations in place on geographic features, consider temporary reprojection (Reprojector) to a local coordinate system or using the CommonLocalReprojector.
The Scaler performs 2D and 3D scaling affine transformations, with additional options for specific geometry types and origin handling.
The Offsetter performs 2D and 3D translation affine transformations, with additional coordinate space options (polar and spherical coordinates, in addition to cartesian).
The Rotator and 3DRotator perform rotation affine transformations, with a simplified interface for rotation value, origin (2D) and axis choice (3D).

Configuration

Input Ports

Output Ports

Parameters

Editing Transformer Parameters

Transformer parameters can be set by directly entering values, using expressions, or referencing other elements in the workspace such as attribute values or user parameters. Various editors and context menus are available to assist. To see what is available, click beside the applicable parameter.

How to Set Parameter Values

Defining Values

There are several ways to define a value for use in a Transformer. The simplest is to simply type in a value or string, which can include functions of various types such as attribute references, math and string functions, and workspace parameters.

Using the Text Editor

The Text Editor provides a convenient way to construct text strings (including regular expressions) from various data sources, such as attributes, parameters, and constants, where the result is used directly inside a parameter.

Text Editor

Using the Arithmetic Editor

The Arithmetic Editor provides a convenient way to construct math expressions from various data sources, such as attributes, parameters, and feature functions, where the result is used directly inside a parameter.

Arithmetic Editor

Conditional Values

Set values depending on one or more test conditions that either pass or fail.

Parameter Condition Definition Dialog

Content

Expressions and strings can include a number of functions, characters, parameters, and more.

When setting values - whether entered directly in a parameter or constructed using one of the editors - strings and expressions containing String, Math, Date/Time or FME Feature Functions will have those functions evaluated. Therefore, the names of these functions (in the form @<function_name>) should not be used as literal string values.

Content Types

String Functions	These functions manipulate and format strings.
Special Characters	A set of control characters is available in the Text Editor.
Math Functions	Math functions are available in both editors.
Date/Time Functions	Date and time functions are available in the Text Editor.
Math Operators	These operators are available in the Arithmetic Editor.
FME Feature Functions	These return primarily feature-specific values.
FME Parameters	FME and workspace-specific parameters may be used.
Creating and Modifying User Parameters	Create your own editable parameters.

Dialog Options - Tables

Table Tools

Transformers with table-style parameters have additional tools for populating and manipulating values.

Row Reordering

Enabled once you have clicked on a row item. Choices include:

Add a row
Remove a row
Move current row up one
Move current row down one
Move current row to top
Move current row to bottom

Cut, Copy, and Paste

Enabled once you have clicked on a row item. Choices include:

Cut a row - delete and copy to clipboard
Copy a row to the clipboard
Paste a row from the clipboard

Cut, copy, and paste may be used within a transformer, or between transformers.

Filter

Start typing a string, and the matrix will only display rows matching those characters. Searches all columns. This only affects the display of attributes within the transformer - it does not alter which attributes are output.

Import

Import populates the table with a set of new attributes read from a dataset. Specific application varies between transformers.

Reset/Refresh

Generally resets the table to its initial state, and may provide additional options to remove invalid entries. Behavior varies between transformers.

Note: Not all tools are available in all transformers.

For more information, see Transformer Parameter Menu Options.

Reference

Processing Behavior	Feature-Based
Feature Holding	No
Dependencies	None
Aliases
History

FME Community

The FME Community has a wealth of FME knowledge with over 20,000 active members worldwide. Get help with FME, share knowledge, and connect with users globally.

Search for all results about the Affiner on the FME Community.

Examples may contain information licensed under the Open Government Licence – Vancouver, Open Government Licence - British Columbia, and/or Open Government Licence – Canada.