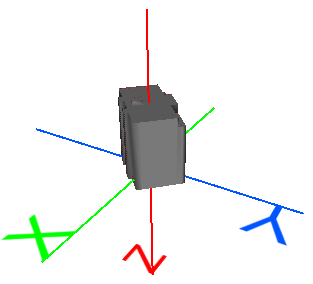
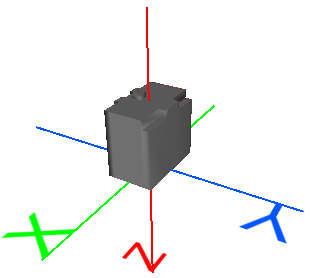
Typical Uses
-
Moving, scaling, and rotating 3D geometry.
How does it work?
The 3DAffiner receives features with any geometry type and moves their x, y and z coordinates according to a specified affine transformation.
A 3D affine transformation is a mathematical method of modifying geometry that:
-
Preserves lines and collinearity: all points on a straight line or plane are still on a straight line or plane after transformation.
-
Preserves parallelism: lines and planes that are initially parallel are still parallel after transformation.
-
May not preserve angles, lengths, or areas, depending on the type of transformation performed.
Scaling, mirroring, rotating, shearing, and translating (relocating or offsetting) are all affine transformations. They can be performed singly or in combination.
The 3DAffiner performs 3D transformations, using this formula:
x' = Ax + By + Cz + D
y' = Ex + Fy + Gz + H
z' = Ix + Jy + Kz + L
Where (x,y,z) are the input coordinates and (x',y',z') are the transformed output coordinates.
|
|
Description |
Formula/Coefficients |
Example |
|---|---|---|---|
|
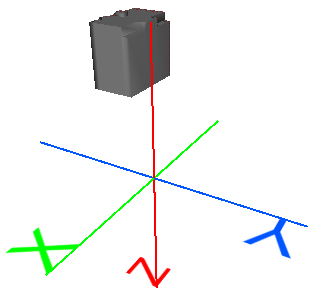
Original 3D Object |
This 3D building model is centered at the origin (0,0,0) and its units are meters. It is not georeferenced. |
|
|
|
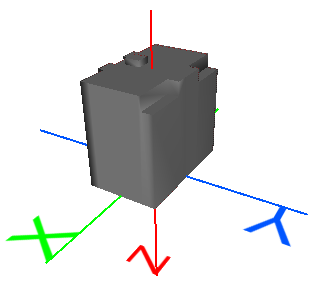
Translate |
Move the geometry a fixed distance. |
x' = 1x + 0y + 0z + D Simplified: x' = x + D D = X offset H = Y offset L = Z offset |
Move object 22 meters along all axes: x' = 1x + 0y + 0z + 22 y' = 0x + 1y + 0z + 22 z' = 0x + 0y + 1z + 22
|
|
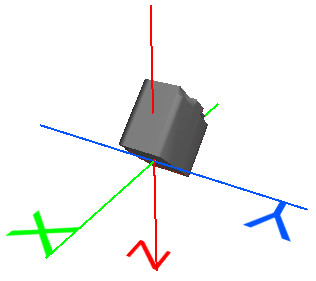
Scale |
Shrink or enlarge the geometry. |
x' = Ax + 0y + 0z + 0 Simplified: x' = Ax A = X scale factor F = Y scale factor K = Z scale factor |
Enlarge object by a scale factor of 1.5: x' = 1.5x + 0y + 0z + 0 y' = 0x + 1.5y + 0z + 0 z' = 0x + 0y + 1.5z + 0
|
|
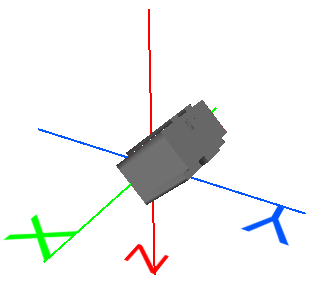
Rotate about X |
Rotate the geometry around the X axis. |
x' = 1x + 0y + 0z + 0 Simplified: x' = x ϴ = Angle in degrees F = cos(ϴ) G = −sin(ϴ) (Note negative value) J = sin(ϴ) K = cos(ϴ) |
Rotate object by 45 degrees around the X axis: x' = 1x + 0y + 0z + 0 y' = 0x + 0.70711y + −0.70711z + 0 z' = 0x + 0.70711y + 0.70711z + 0
|
|
Rotate about Y |
Rotate the geometry around the Y axis. |
x' = cos(ϴ)x + 0y + sin(ϴ)z + 0 Simplified: x' = cos(ϴ)x + sin(ϴ)z ϴ = Angle in degrees A = cos(ϴ) C = sin(ϴ) I = −sin(ϴ) (Note negative value) K = cos(ϴ) |
Rotate object by 45 degrees around the Y axis: x' = 0.70711x + 0y + 0.70711z + 0 y' = 0x + 1y + 0z + 0 z' = -0.70711x + 0y + 0.70711z + 0
|
|
Rotate about Z |
Rotate the geometry around the Z axis. |
x' = cos(ϴ)x + −sin(ϴ)y + 0z + 0 Simplified: x' = cos(ϴ)x − sin(ϴ)z ϴ = Angle in degrees A = cos(ϴ) B = −sin(ϴ) (Note negative value) E = sin(ϴ) F = cos(ϴ) |
Rotate object by 45 degrees around the Z axis: x' = 0.70711x + −0.70711y + 0z + 0 y' = 0.70711x + 0.70711y + 0z + 0 z' = 0x + 0y + 1z + 0
|
Usage Notes
-
To perform affine transformations in place on geographic features, consider temporary reprojection (Reprojector) to a local coordinate system or using the CommonLocalReprojector.
-
The Scaler performs 2D and 3D scaling affine transformations, with additional options for specific geometry types and origin handling.
-
The Offsetter performs 2D and 3D translation affine transformations, with additional coordinate space options (polar and spherical coordinates, in addition to cartesian).
-
The Rotator and 3DRotator perform rotation affine transformations, with a simplified interface for rotation value, origin (2D) and axis choice (3D).
Configuration
Input Ports
This transformer accepts any feature. Arcs and ellipses will be stroked to lines and polygons (respectively) before undergoing the transformation.
Output Ports
Features transformed according to parameter selections.
Parameters
|
A |
Provide values for all coefficients and constants in the affine formula: x' = Ax + By + Cz + D y' = Ex + Fy + Gz + H z' = Ix + Jy + Kz + L Where (x,y,z) are the input coordinates and (x',y',z') are the transformed output coordinates. If a value is not needed for the required transformation, the value should be zero (0). |
Editing Transformer Parameters
Using a set of menu options, transformer parameters can be assigned by referencing other elements in the workspace. More advanced functions, such as an advanced editor and an arithmetic editor, are also available in some transformers. To access a menu of these options, click  beside the applicable parameter. For more information, see Transformer Parameter Menu Options.
beside the applicable parameter. For more information, see Transformer Parameter Menu Options.
Defining Values
There are several ways to define a value for use in a Transformer. The simplest is to simply type in a value or string, which can include functions of various types such as attribute references, math and string functions, and workspace parameters. There are a number of tools and shortcuts that can assist in constructing values, generally available from the drop-down context menu adjacent to the value field.
Using the Text Editor
The Text Editor provides a convenient way to construct text strings (including regular expressions) from various data sources, such as attributes, parameters, and constants, where the result is used directly inside a parameter.
Using the Arithmetic Editor
The Arithmetic Editor provides a convenient way to construct math expressions from various data sources, such as attributes, parameters, and feature functions, where the result is used directly inside a parameter.
Conditional Values
Set values depending on one or more test conditions that either pass or fail.
Parameter Condition Definition Dialog
Content
Expressions and strings can include a number of functions, characters, parameters, and more.
When setting values - whether entered directly in a parameter or constructed using one of the editors - strings and expressions containing String, Math, Date/Time or FME Feature Functions will have those functions evaluated. Therefore, the names of these functions (in the form @<function_name>) should not be used as literal string values.
| These functions manipulate and format strings. | |
|
Special Characters |
A set of control characters is available in the Text Editor. |
| Math functions are available in both editors. | |
| Date/Time Functions | Date and time functions are available in the Text Editor. |
| These operators are available in the Arithmetic Editor. | |
| These return primarily feature-specific values. | |
| FME and workspace-specific parameters may be used. | |
| Creating and Modifying User Parameters | Create your own editable parameters. |
Dialog Options - Tables
Transformers with table-style parameters have additional tools for populating and manipulating values.
|
Row Reordering
|
Enabled once you have clicked on a row item. Choices include:
|
|
Cut, Copy, and Paste
|
Enabled once you have clicked on a row item. Choices include:
Cut, copy, and paste may be used within a transformer, or between transformers. |
|
Filter
|
Start typing a string, and the matrix will only display rows matching those characters. Searches all columns. This only affects the display of attributes within the transformer - it does not alter which attributes are output. |
|
Import
|
Import populates the table with a set of new attributes read from a dataset. Specific application varies between transformers. |
|
Reset/Refresh
|
Generally resets the table to its initial state, and may provide additional options to remove invalid entries. Behavior varies between transformers. |
Note: Not all tools are available in all transformers.
Reference
|
Processing Behavior |
|
|
Feature Holding |
No |
| Dependencies | None |
| Aliases | |
| History |
FME Community
The FME Community is the place for demos, how-tos, articles, FAQs, and more. Get answers to your questions, learn from other users, and suggest, vote, and comment on new features.
Search for all results about the 3DAffiner on the FME Community.
Examples may contain information licensed under the Open Government Licence – Vancouver and/or the Open Government Licence – Canada.
3D building model by Berlin Partner für Wirtschaft und Technologie GmbH.