Supported Geometries

All FME features have an attribute called fme_geometry, which indicates the coordinates of the feature, and an attribute called fme_type, which defines how those coordinates are interpreted.

The FME Geometry Model supports the following types of features:

Points

Point geometries are features represented by a single coordinate.

A simple point feature has just an x/y coordinate; but there are other point geometry subtypes.
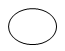
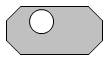
Ellipses are basically circle or oval features; like an arc but closing on themselves, so don’t require a start angle or sweep angle.
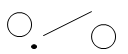
A Point Cloud is comprised of a large number of unconnected point features.
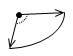
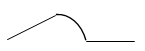
Arc features are often defined by an x/y coordinate at their center point, plus a mathematical definition of arc radius and sweep angles.
An alternate arc definition is the center point, plus the two end point X/Y coordinates
A further arc definition is the two end points, plus the mid-point of the arc ‘line’.

Text

Text features represent the position of an annotation.

Text features’ definition optionally includes size, rotation, and justification. Although text features are traditionally thought of as a single x/y coordinate, they can have a line or other geometry.

North Road

Lines

A line is a series of points strung together to form a chain.

The simplest form of line geometry is a two-point line; that is, it has a start coordinate and an end coordinate but no intermediate points.
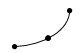
A polyline feature is a multi-point line; that is, it has a start coordinate and an end coordinate plus a number of intermediate points.

Polygons

A polygon feature is a series of points strung together, whose first and last points coincide to form a closed shape.

A simple polygon forms a single closed shape.
A donut is made up of an outer boundary to define a perimeter and an inner boundary to represent a hole within it.

Aggregates

An aggregate is a defined set of any of the above features. It is also sometimes known as a ‘collection’ or ‘group’.

A homogeneous aggregate is made up of features of the same geometry type.
A non-homogeneous aggregate is made up of features with differing geometry types.

Raster

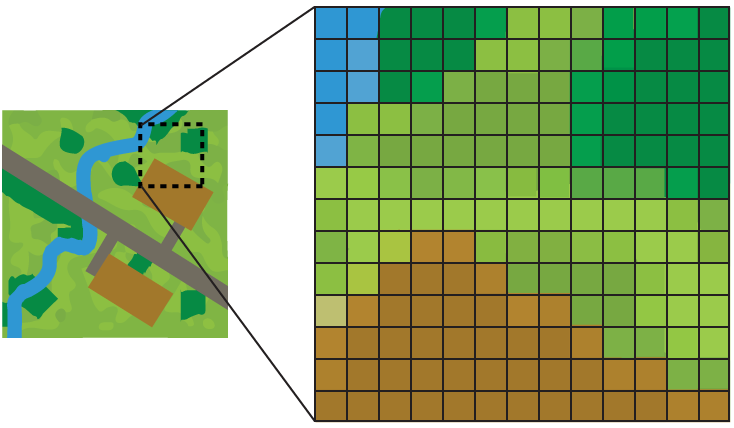
A raster geometry feature is a set of pixels or cells in a grid.

A Raster feature is a set of cells, not an individual cell. Cells do not generally have attributes, but may possess a single value or color.

Paths

A path (also called chain) is a linear object made up of a number of features connected together.

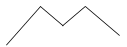
A path can be made up of features of the same geometry type or, more commonly, of different geometry types; for example, line-arc-line.

Surfaces

Surfaces are three-dimensional planar features. There are many types of surfaces supported in FME, including faces (see illustration below), meshes, triangle strips, and triangle fans.

A face is one example of a surface feature. It’s a planar polygon or donut stored as a true 3D feature.
A surface may contain holes, in much the same way as a donut polygon.

Solids

Solids are three-dimensional entities. There are many types of solids supported in FME. These include boxes (see illustration below), extrusions, b-rep solids, and CSGs (see illustration). Although similar, these different types of solids are required for compatibility with the full range of FME-supported formats.

A Box is one example of a solid feature. Like a hole or donut, it can contain a void within it.
A CSG (Constructive Solid Geometry) is a complex object made up of a set of solids upon which a Boolean operation has been carried out. Boolean operations that can be carried out are Union (right), Difference, and Intersection.

3D Multiples

Multiples are the 3D equivalent of aggregates. They are always homogeneous, which means that they are made up of the same type.

Multi-surfaces are one example of this type of geometry. They are multiple surface features related as a collection. A Composite Surface is a multi-surface where all items are connected topologically.

Named Geometries

All features can be given a name to their geometry. This is achieved with the transformers GeometryPropertySetter, GeometryPropertyExtractor, and GeometryPropertyRemover.

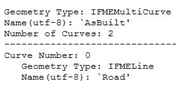
Naming can be recursive; for example, this feature is an aggregate named 'AsBuilt', whereas its components are named Road.