FME Form: 2024.1
Mesh
A mesh is a special collection of simple facets or parts. These parts need not have any spatial or topological relationship between each other, although many systems work with contiguous meshes.
A mesh consists of separate parts that use references to a common vertex pool, vertex normal pool, and texture coordinate pool. The individual parts of the mesh represent faces with a planar polygon structure. See the documentation for Faces on:
- How vertex order affects surface normal and front/back surface determination.
- How planar characteristics of each part are often expected, but not strictly enforced.
The parts of a mesh are defined by indices into the common pools. By allowing reuse of shared vertices, the physical representation size of a mesh can be smaller than an equivalent collection of surfaces.
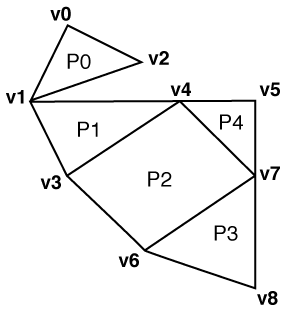
In the example, P0 to P4 are mesh parts, and vertices v0 to v8 are stored in a common vertex pool. The definition of a part is provided by a list of vertex indices that reference the common vertex pool. For example, P2 is defined by the vertex index list containing the indices 6, 7, 4, 3, and 6.
Meshes do not have measures.
Optionally, meshes may possess a transformation matrix. Meshes may also have front or back appearances, and may be single or double sided. Mesh parts themselves may also have front or back appearances, and may be single or double sided.