Uses the Sherbend algorithm to simplify lines by reducing unnecessary details based on the analysis of the line’s bends.
Sherbend is a constraint-based algorithm that preserves the spatial relationship of the lines and points in the input data. The Sherbend algorithm iteratively generalizes the bends in a line by using the Diameter parameter to select bends for generalization. The generalization process may eliminate, reduce, or combine bends, while resolving conflicts.
The strategy for generalizing bends in a line is as follows:
- Calculate the area of a reference circle whose diameter is specified by the Diameter parameter.
- For each line, determine the locations of the bends.
- For each bend, calculate its perimeter. Next, construct a circle whose circumference is equal to that perimeter. Finally, determine the adjusted area of the bend, which is 75% of the area of that circle.
- For each bend, generalize the bend if its area is below the area of the reference circle and spatial constraints are met.
- Repeat the above steps until there are no more bends to generalize.
Input Ports
Lines
Input lines for generalization. They are assumed to not self-intersect or intersect with another line or point.
Points
Input points for the sidedness constraint. When the “Sidedness” constraint is enabled, these points will prevent a bend generalization if that would change the spatial relationship between the bend and the points.
Output Ports
Lines
The generalized lines.
Conflicts
Bends that, if generalized, would violate the selected constraint.
<Rejected>
Invalid input features will be output to the <Rejected> port.
Parameters
Transformer
Group By
Only lines and points in the same group are subject to constraint checking. If no group is specified, all lines and points are placed in the same group.
Group By Mode
Process At End (Blocking): This is the default behavior. Processing will only occur in this transformer once all input is present.
Process When Group Changes (Advanced): This transformer will process input groups in order. Changes of the value of the Group By parameter on the input stream will trigger processing on the currently accumulating group. This may improve overall speed (particularly with multiple, equally-sized groups), but could cause undesired behavior if input groups are not truly ordered.
Considerations for Using Group By
There are two typical reasons for using Process When Group Changes (Advanced) . The first is incoming data that is intended to be processed in groups (and is already so ordered). In this case, the structure dictates Group By usage - not performance considerations.
The second possible reason is potential performance gains.
Performance gains are most likely when the data is already sorted (or read using a SQL ORDER BY statement) since less work is required of FME. If the data needs ordering, it can be sorted in the workspace (though the added processing overhead may negate any gains).
Sorting becomes more difficult according to the number of data streams. Multiple streams of data could be almost impossible to sort into the correct order, since all features matching a Group By value need to arrive before any features (of any feature type or dataset) belonging to the next group. In this case, using Group By with Process At End (Blocking) may be the equivalent and simpler approach.
Note: Multiple feature types and features from multiple datasets will not generally naturally occur in the correct order.
As with many scenarios, testing different approaches in your workspace with your data is the only definitive way to identify performance gains.
Parameters
Diameter
This parameter specifies the diameter of the reference circle (described at the beginning of this documentation), which roughly describes the width of a bend below which the bend will be generalized. Different lines can have different diameters specified as an attribute. The bigger the diameter, the more likely bends will be generalized.
Spatial Constraints
Enables spatial constraints, which are only applied to lines and points in the same group.
- None: constraints will not be applied.
- Self Intersection prevents a line from intersecting with itself, with the assumption that input lines do not self-intersect when entering SherbendGeneralizer.
- Self, Line-Line Intersection prevents a line from intersecting with itself or another line, with the assumption that no input line self-intersects or intersects another line when entering SherbendGeneralizer.
- Self, Line-Line Intersection, Sidedness, in addition to maintaining non-intersecting lines, maintains the relative positioning of all lines and points. For example, if a line is entirely on the right side of another line, that line will remain entirely on the right side of that other line after the generalization process.
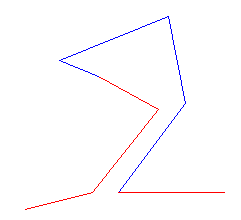
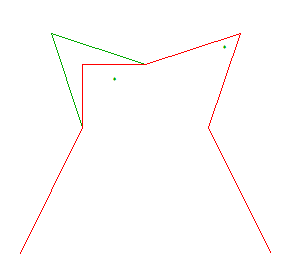
In this diagram, the blue bend cannot be generalized as it would violate the “Sidedness” constraint:
In this diagram, the blue bend cannot be generalized as it would violate the “Self Intersection” constraint:
Preserve Endpoints in Closed Lines
This parameter, if set to No, will re-order (rotate) the coordinate list of each closed line in an attempt to improve the quality of generalization. To preserve juncture connectivity, the transformer must ensure that the starting and end coordinates of every line are kept stationary. Therefore, if it is important to keep the positions of the first and last coordinates in a closed line (perhaps because they are on a juncture), this parameter should be set to Yes.
If this parameter is set to Yes, the endpoints of a line will not be moved. This behavior allows the preservation of juncture connectivity.
Examples
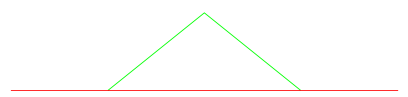
In this example, a bend is reduced (green = input, red = output):
In this example, a bend is eliminated:
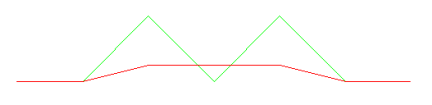
In this example, three bends are combined into one:
The following diagram illustrates the generalization process on a single line in a real-world dataset:
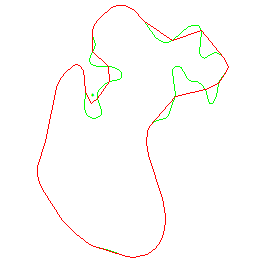
This example illustrates the generalization process on a set of contours:
Additional Information
The aim of line generalization is to reduce the details on a line for representation at a smaller scale. While the well-known Douglas-Peucker algorithm, is good at reducing the number of points in a line, it is not so good at removing unnecessary details in a line. The Generalizer transformer contains a selection of algorithms under its parameters including the Douglas-Peucker algorithm.
In comparison, the Sherbend algorithm is well suited for the generalization of natural features (contours, lakes, rivers, wooded areas, etc.) because it preserves the general shape of the line. Moreoever, if spatial constraints are enabled, the spatial relationship between the input entities are preserved. The Douglas-Peucker algorithm with a small tolerance is often used before or after Sherbend to further reduce the number of points to further fulfill the goals of generalization.
Performance and Usage Notes
- The Sherbend algorithm iteratively detects and generalizes bends, and then detects and resolves spatial conflicts. The generalized lines from one iteration are passed to the next iteration until the lines cannot be generalized further. Due to this iterative process, the algorithm is time-intensive, which is a tradeoff to improved accuracy and quality of generalization.
- Constraint checking is a highly time-intensive operation. Use constraints only as necessary.
- To generalize each feature independently, consider using the Generalizer transformer.
Editing Transformer Parameters
Using a set of menu options, transformer parameters can be assigned by referencing other elements in the workspace. More advanced functions, such as an advanced editor and an arithmetic editor, are also available in some transformers. To access a menu of these options, click 
beside the applicable parameter. For more information, see Transformer Parameter Menu Options.
Transformer Categories
FME Licensing Level
FME Professional edition and above
Search FME Community
Search for samples and information about this transformer on the FME Community.