Spatial Relations Defined

Spatial relationships are described by predicates - keywords that indicate the type of relationship each piece of geometry has with another. These relationships are defined by the OGC (Open Geospatial Consortium), and are interpreted in FME.

Spatial relationships are based on how three components of a feature intersect - or don't intersect - with another feature. Each feature has an INTERIOR, BOUNDARY, and EXTERIOR. These terms are defined below for various geometry types. How these components interact determines the type of spatial relationship features have, and which predicates they match.

Spatial relations are undefined for geometries that are not OGC valid or aggregate geometries. For definitive documentation on spatial relations, please consult the OGC documentation. For more information on how FME handles aggregate and multi geometries, see below.

Spatial Predicates

Predicates - such as Intersects, Contains, Overlaps, and more - are commonly used in spatial joins. The SpatialFilter and SpatialRelator allow explicit spatial query construction using predicates.

Each of the supported predicates is described here, along with some associated examples and pattern matrices. Note that the examples are not exhaustive: there may be entirely different situations where a given predicate is true.

Spatial Predicates with Examples

In these examples, the base is labeled "A" and the candidate is labeled "B".

Geometry examples are shown comparing points, lines, and areas. Bases are in blue, candidates in yellow. Examples showing multiple bases or candidates do not represent multi or aggregate geometry, rather, they indicate alternate scenarios that match the predicate.

Predicate	Description	Pattern Matrix*
Intersects	The two features are not disjoint, as defined next.
Disjoint	The boundaries and interiors do not intersect.
Equals	The features have the same boundary and the same interior.
Touches	The boundaries may intersect or one boundary may intersect the other interior. The interiors do not touch. Undefined for point/point.


Crosses	The interiors intersect and the base’s interior intersects the candidate’s exterior. Or in the case of line/line, the intersection of the interiors forms a point. Undefined for point/point or area/area. Undefined for aggregate/multi geometries.
		For two lines:

Overlaps	The interiors intersect, but neither feature is contained by the other, nor are the features equal. Undefined for point/line, point/area, or line/area. Undefined for aggregate/multi geometries.
		For two lines:

Contains	The interiors intersect and no part of the candidate's interior or boundary intersects the base's exterior. It is possible for the boundaries to intersect. Inverse of WITHIN.
Within	The interiors intersect and no part of the base's interior or boundary intersects the candidate's exterior. It is possible for the boundaries to intersect. Inverse of CONTAINS.

* See Dimensionally Extended 9 Intersection Matrix (DE-9IM) below.

Aggregates and Multi Geometry

Spatial relationships for aggregate and multi geometries are not clearly defined, and should be used with care. Where reasonable, FME uses an intuitive definition to analyze these relationships, however, these are not well-known definitions according to any public standard.

Aggregate and Multi Geometry Behaviors

All relationships are defined for all combinations of multi-geometry types, with the exception of IFMEMultiText, IFMEMultiSurface, and IFMEMultiSolid, which are not defined for any relationship. Any places where a relationship differs from this rule are noted.

Intersects	A geometry intersect a multi if, and only if, at least one part of the multi intersects the geometry. This is the same of a multi intersecting a geometry. A multi intersects another multi if, and only if, at least one part from one multi intersects at least on part of the other multi.
Disjoint	A geometry is disjoint from a multi if, and only if, the geometry is disjoint from all parts of the multi. This is the same of a multi disjoint from a geometry. A multi is disjoint from another multi if, and only if, all parts from each multi are disjoint from all points of the other multi.
Equals	A multi-geometry can only be equal to another multi-geometry of the same type (for example, IFMEAggregate with IFMEAggregate, or IFMEMultiCurve with IFMEMultiCurve). Two multi-geometries are equal if, and only if, the number of parts in each multi is the same, and each part from one multi has an equal match in the other multi, with no ‘double matches’ (i.e. no part of either multi can be left without a match).
Touches	A geometry touches a multi if, and only if, at least one part of the multi touches the geometry, and no other non-touching parts intersect with the geometry. This is the same of a multi touching a geometry. A multi touches another multi if, and only if, at least one part of each multi touches a part of the other, and no non-touching parts intersect parts of the other.
Crosses	Is not supported for multi/aggregate geometries.
Overlaps	Is not supported for multi/aggregate geometries.
Contains	A geometry contains a multi if, and only if, the geometry contains all parts of the multi. A multi contains a geometry if, and only if, at least one part of the multi contains the geometry. This not defined for: IFMEMultiPoint Contains IFMEGeometry A multi contains another multi if, and only if, at least one part of the container multi contains all parts of the containee. This not defined for: IFMEMultiPoint Contains Multi-geometry
Within	A geometry is within a multi if, and only if, the geometry is within at least one part of the multi. This is not defined for: IFMEGeometry Within IFMEMultiPoint A multi is within a geometry if, and only if, every part of the multi is within the geometry. A multi is within another multi if, and only if, every part of the contained multi is within at least one part of the container multi. This is not defined for: Multi-geometry Within IFMEMultiPoint

Dimensionally Extended 9 Intersection Matrix (DE-9IM)

The comparison of two features produces a 3 x 3 matrix known as the Dimensionally Extended 9 Intersection Matrix (DE-9IM). These matrices may also be represented as a 9-character string.

Matrix examples are included in the Predicates table above.

Using the DE-9IM

		Candidate
		Interior	Boundary	Exterior
Base	Interior	x₀	x₁	x₂
	Boundary	x₃	x₄	x₅
	Exterior	x₆	x₇	x₈

The value of each element of the matrix indicates the dimension of the geometry produced by intersecting the given parts of the two features. The dimension is one of the following:

-1 there is no interaction

0 the intersection produces a point

1 the intersection produces a line

2 the intersection produces a surface

So for instance, if x₁ is 1, then the intersection of the base's interior with the candidate's boundary produces a line. This could occur when both features are polygons and they overlap.

Each of the predicates can be defined in terms of what the intersection matrix of the two features must look like. For this, use a pattern matrix. Each element of the pattern matrix can be one of the following:

* the value of this element may be anything (-1, 0, 1, or 2)

T the value of this element must be 0, 1, or 2

F the value of this element must be -1

0 the value of this element must be 0

1 the value of this element must be 1

2 the value of this element must be 2

The pattern matrix for the disjoint predicate is:

This means that neither feature's interior or boundary may interact with the other's interior or boundary.

String Representations of Intersection Matrices

Any intersection matrix can be represented as a 9-character string. To generate the string representation of a particular intersection matrix, take each element starting from the top-left, going left-to-right for each row.

For example, the string representation of the intersection matrix for the disjoint predicate (as seen above) is “FF*FF****”.

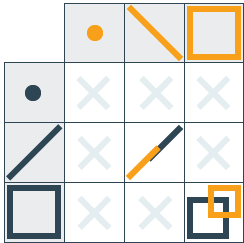
BOUNDARY	Point	Empty set.
	Line	CURVE_BOUNDARY_RULE ENDPOINTS_MOD2 The boundary is the set of all endpoints that occur an odd number of times. For a simple linear feature (that is, not a multicurve), this means the boundary is comprised of the start and end points, unless the line is closed (the start and end are the same point), in which case the boundary is the empty set. (This is the default if CURVE_BOUNDARY_RULE is unspecified.) CURVE_BOUNDARY_RULE ENDPOINTS_ALL The boundary is the set of all endpoints, regardless of the number of times they occur in the geometry.
	Area	The border of a polygon, including the border of the holes.
INTERIOR	Point	The point location.
	Line	The entire line except its boundary as determined above.
	Area	The inner surface of the polygon.
EXTERIOR	Point	Everything that is not on the BOUNDARY or the INTERIOR.
	Line
	Area